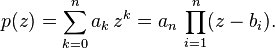- Asíntotas horizontales (paralelas al eje OX)Si existe el límite: :La recta “y = b” es la asíntota horizontal.Ejemplo:
 es la asíntota horizontal.
es la asíntota horizontal. - Asíntotas oblicuas (inclinadas)Si existen los límites: :
 La recta “y = mx+n” es la asíntota oblicua.Ejemplo:
La recta “y = mx+n” es la asíntota oblicua.Ejemplo:
 es la asíntota oblicua.
es la asíntota oblicua.
domingo, 28 de abril de 2013
Criterios de existencia de las asintotas horizontales y oblicuas.
sábado, 27 de abril de 2013
Asíntotas verticales.
Las asíntotas verticales son rectas verticales a las cuales la función se va acercando indefinidamente sin llegar nunca a cortarlas.
Las asíntotas verticales son rectas de ecuación: x = k.
K son los puntos que no pertenecen al dominio de la función (en las funciones racionales).
Ejemplo:

Asíntotas horizontales.
Las asíntotas horizontales son rectas horizontales a las cuales la función se va acercando indefinidamente.
Las asíntotas horizontales son rectas de ecuación: y = k.

Ejemplo:

Dominio de definición de una función racional.
En matemáticas, el dominio (conjunto de definición o conjunto de partida) de una función  es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota
es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota  o bien
o bien 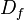 . En
. En  se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío.
se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío.
 es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota
es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota  o bien
o bien 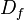 . En
. En  se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío.
se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío.Función racional.
En matemáticas, una función racional es una función que puede ser expresada de la forma:
donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen su dominio de definición en todos los valores de x que no anulen el denominador.
La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.
Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.
Teorema fundamental del álgebra.
El teorema se enuncia comúnmente de la siguiente manera:
|
Es ampliamente conocido también el enunciado: Un polinomio en una variable, no constante y con coeficientes complejos, tiene tantas raíces como indica su grado, contando las raíces con sus multiplicidades. En otras palabras, dado un polinomio complejo p(z) de grado n ≥ 1, la ecuación p(z) = 0 tiene exactamente n soluciones complejas, contando multiplicidades.
Otras formas equivalentes del teorema son:
- El cuerpo de los complejos es cerrado para las operaciones algebraicas.
- Todo polinomio complejo de grado n ≥ 1 se puede expresar como un producto de n polinomios lineales, es decir
División Sintética.
La división sintética se realiza para simplificar la división de un polinomio entre otro polinomio de la forma x – c, logrando una manera mas compacta y sencilla de realizar la división.
Ilustraremos como el proceso de creación de la división sintética con un ejemplo:
Comenzamos dividiéndolo normalmente
Teorema del factor y del residuo.
Si se divide la función polinomial ƒ(x) entre el binomio x - a donde a es un número real, el residuo es igual a ƒ(a).
El teorema del residuo indica que el resultado de evaluar numéricamente una función polinomial para un valor a es igual al residuo de dividir el polinomio entre x - a. Un ejemplo de esto se ilustra en la parte de arriba. Se recomienda que el lector realice otras comprobaciones. Una conclusión muy importante del teorema del residuo es se puede evaluar numéricamente una función polinomial usando la división sintética.
A partir de lo anterior, si ƒ(a) = 0, entonces x - a es un factor del polinomio porque el residuo es cero. Cuando se encuentra un valor de x para el cual ƒ(x) = 0 se ha encontrado una raiz del polinomio, en el supuesto anterior, a es una raiz del polinomio.
Si a es una raiz de ƒ(x), entonces x - a es un factor del polinomio, donde a es un número real.
Aqui podemos observar la importancia de conocer el valor del residuo, ya que si éste es igual a cero, nos va a indicar que hemos encontrado un factor del polinomio y con él, una raiz del polinomio (una solución a la ecuación polinomial ƒ(x) = 0).
Ceros y raíces de la función.
En matemática, se conoce como raíz (o cero) de una función (definida sobre un cierto cuerpo algebraico) f(x) a todo elemento x perteneciente al dominio de dicha función tal que se cumpla:
.
Por ejemplo, dada la función:
Planteando y resolviendo la ecuación:
Se tiene que 2 y 4 son raíces (ver ecuación de segundo grado) ya que f(2) = 0 y f(4) = 0.
Parámetros de las funciones de grado: cero, uno y dos.
Características de las funciones polinomiales de grados: cero, uno y dos.



Representación gráfica de funciones de grados: cero, uno y dos.
Representación gráfica de funciones polinómicas de grado uno
La forma de esta función de grado uno es la ecuación de la línea recta, que tiene su gráfica como aparece de forma oblicua.y = m x + b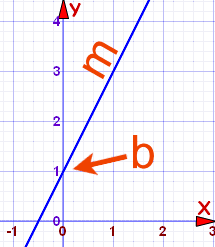
Representación gráfica de funciones polinómicas de grado 2
Las funciones polinómicas de grado 2 son del tipo  , con
, con  . Sus representaciones gráficas son las famosas parábolas. Hay dos posibles representaciones que dependen del signo de
. Sus representaciones gráficas son las famosas parábolas. Hay dos posibles representaciones que dependen del signo de  . Son éstas:
. Son éstas:
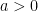



Representación gráfica de funciones polinómicas de grado 3
Las funciones polinómicas de grado 3 son del tipo 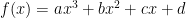 , con
, con  . Hay cuatro posibles representaciones gráfica de este tipo de funciones que dependen del signo de
. Hay cuatro posibles representaciones gráfica de este tipo de funciones que dependen del signo de  y de la relación entre
y de la relación entre 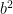 y
y  . Por tanto, para poder representarlas debemos tener en cuenta sus coeficientes. Os dejo una tabla con las cuatro gráficas posibles:
. Por tanto, para poder representarlas debemos tener en cuenta sus coeficientes. Os dejo una tabla con las cuatro gráficas posibles:
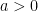








Representación gráfica de funciones polinómicas de grado 2
Las funciones polinómicas de grado 2 son del tipo  , con
, con  . Sus representaciones gráficas son las famosas parábolas. Hay dos posibles representaciones que dependen del signo de
. Sus representaciones gráficas son las famosas parábolas. Hay dos posibles representaciones que dependen del signo de  . Son éstas:
. Son éstas:
 |  |
Representación gráfica de funciones polinómicas de grado 3
Las funciones polinómicas de grado 3 son del tipo 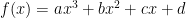 , con
, con  . Hay cuatro posibles representaciones gráfica de este tipo de funciones que dependen del signo de
. Hay cuatro posibles representaciones gráfica de este tipo de funciones que dependen del signo de  y de la relación entre
y de la relación entre 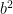 y
y  . Por tanto, para poder representarlas debemos tener en cuenta sus coeficientes. Os dejo una tabla con las cuatro gráficas posibles:
. Por tanto, para poder representarlas debemos tener en cuenta sus coeficientes. Os dejo una tabla con las cuatro gráficas posibles:
 |  | |
 |  |
Suscribirse a:
Entradas (Atom)